Sadarkah kamu jika hidup itu penuh dengan kemungkinan? Misalnya saja kamu mengikuti seleksi masuk perguruan tinggi. Apakah kamu bisa memastikan kamu lolos atau tidak lolos? Tentu tidak, ya. Hasil akhirnya hanya ada dua kemungkinan, lolos atau tidak lolos. Kemungkinan kamu lolos 50% dan kemungkinan tidak lolos juga 50%. Di dalam Matematika, kemungkinan-kemungkinan semacam itu disebut sebagai peluang. Apa yang dimaksud peluang? Daripada penasaran, yuk simak selengkapnya!
Pengertian Peluang Suatu Kejadian
Peluang adalah nilai (kuantitas) untuk menyatakan seberapa besar
terjadinya suatu peristiwa. Peluang juga biasa disebut sebagai probabilitas.
Pembahasan peluang ini sangat erat kaitannya dengan kehidupan sehari-hari.
Mengingat, hidup itu penuh dengan kemungkinan-kemungkinan. Contoh penerapan
teori peluang dalam kehidupan sehari-hari bisa kamu ambil dari hal sepele,
yaitu pelemparan dadu. Apakah kamu bisa memastikan nilai mata dadu yang muncul
setelah dilemparkan? Tentu tidak, ya. Tiga hal yang harus kamu ketahui untuk
menentukan peluang, yaitu percobaan, ruang sampel, dan kejadian.
Pengertian Percobaan
Percobaan adalah suatu
kegiatan yang menghasilkan nilai suatu peluang. Misalnya proses pelemparan dua
buah dadu, pengambilan bola di dalam kotak, pengambilan kartu, dan sebagainya.
Pengertian
Ruang Sampel
Ruang sampel adalah semua
hasil yang mungkin terjadi dari suatu percobaan. Ruang sampel dinotasikan
sebagai S dan banyaknya elemen ruang sampel dinotasikan n(S). Misalnya, kamu
melemparkan dua buah koin, kemungkinan hasil yang muncul adalah {(A,G), (G,A),
(A,A), (G,G)}.
Pengertian
Kejadian
Kejadian adalah hasil
diharapkan terjadi pada ruang sampel. Kejadian dinotasikan sebagai A. Dengan
demikian, banyaknya kejadian A dinotasikan sebagai n(A). Misalnya, berapakah
banyaknya kejadian muncul 1 A dan 1 G pada pelemparan dua buah koin? Munculnya
1 A dan 1 G bisa diperoleh dari {(A,G), (G,A)}. Dengan demikian, banyaknya
kejadian muncul 1 A dan 1 G adalah 2.
Peluang Suatu Kejadian
Peluang suatu kejadian
erat kaitannya dengan pembahasan tentang ruang sampel dan kejadian. Peluang
suatu kejadian adalah perbandingan antara jumlah suatu kejadian (n(A)) dan
semua kemungkinan yang ada (n(S)). Secara matematis, rumus peluang suatu
kejadian A pada ruang sampel S adalah sebagai berikut.
Dengan:
P(A) = peluang terjadinya A;
n(A) = banyaknya elemen kejadian A; dan
n(S) = banyaknya elemen ruang sampel S.
Peluang terjadinya suatu kejadian itu berada di rentang 0 dan 1. Nilai 0
menunjukkan kejadian yang mustahil terjadi atau banyaknya elemen A = 0.
Sementara itu, nilai 1 menunjukkan kejadian yang pasti terjadi atau banyaknya
elemen A sama dengan ruang sampel. Secara matematis,
Contoh kejadian yang mustahil terjadi;
- Misalkan pada pelemparan sebuah dadu, kejadian muncul angka 7 mustahil terjadi.
- Contoh yang lain, tidak mungkin bagi laki-laki mendapat haid atau hamil dan melahirkan bukan karena tidak mempunyai sel telur dan rahim jadi tidak akan terjadi atau tidak akan pernah mempunyai peluang untuk haid atau hamil dan melahirkan.
Contoh kejadian yang pasti terjadi;
- Misalkan pada pelemparan sebuah dadu, kejadian muncul salah satu dari enam bilangan asli pertama pasti terjadi.
- semua mahluk hidup pasti akan mati. Ini kejadian yang pasti bukan? Tuhan tidak menciptakan mahluknya untuk hidup abadi, meskipun ada yang berusia ratusan tahun atau bahkan pohon berusia ribuan tahun mungkin pada akhirnya mereka semua akan mati jika saatnya tiba.
Contoh Soal Peluang Suatu Kejadian
Adapun contoh peluang
suatu kejadian adalah sebagai berikut.
Pada pelemparan sebuah dadu, tentukan peluang muncul mata
dadu bilangan prima!
Pembahasan:
Pada pelemparan sebuah
dadu, banyaknya sampel yang mungkin terjadi adalah {1, 2, 3, 4, 5, 6} → n(S) =
6
Mata dadu bilangan prima
(A) = {2, 3, 5} → n(A) = 3
Dengan demikian, peluang
muncul mata dadu bilangan prima adalah sebagai berikut.
Jadi, peluang muncul mata dadu bilangan prima adalah 0,5.
Dari soal yang sama, berapakah peluang terambilnya mata dadu faktor dari
6?
Pada pelemparan sebuah dadu, banyaknya sampel yang mungkin terjadi
adalah {1, 2, 3, 4, 5, 6} → n(S) = 6
Mata dadu faktor dari 6 (A) = {1, 2, 3, 6} → n(A) = 4
Dengan demikian, peluang muncul mata dadu faktor dari 6 adalah sebagai
berikut.
Jadi, peluang muncul mata dadu faktor dari 6 adalah 2/3.
itulah pembahasan mengenai peluang suatu kejadian. Semoga bermanfaat :)
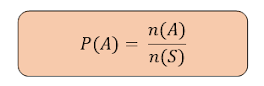
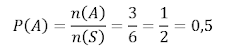

Tidak ada komentar:
Posting Komentar